Hyperbolic Paraboloid Roof Structure Pdf
Contents • • • • • • • • • • • • Properties and applications [ ] Elliptic paraboloid [ ] With a = b an elliptic paraboloid is a paraboloid of revolution: a surface obtained by revolving a around its axis. It is the shape of the used in, dishes, and the like; and is also the shape of the surface of a rotating liquid, a principle used in and in making solid telescope mirrors (see ). This shape is also called a circular paraboloid. There is a point called the (or focal point) on the axis of a circular paraboloid such that, if the paraboloid is a mirror, light from a point source at the focus is reflected into a parallel beam, parallel to the axis of the paraboloid. This also works the other way around: a parallel beam of light incident on the paraboloid parallel to its axis is concentrated at the focal point.
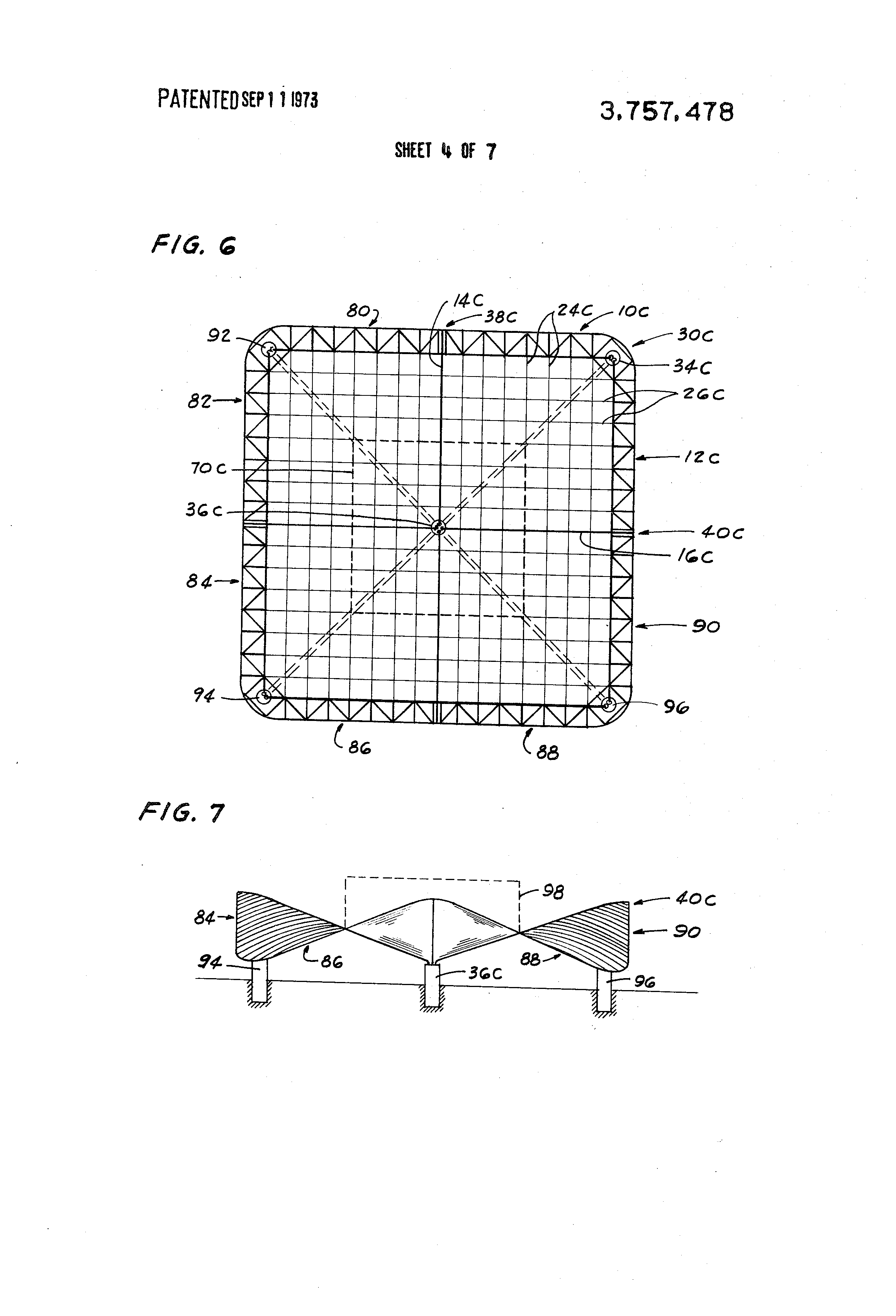
Ms Lync Windows Xp more. This applies also for other waves, hence. Ansys Hpc Pack License. For a geometrical proof, click. Rotating water in a glass Hyperbolic paraboloid [ ] The hyperbolic paraboloid is a: it contains two families of mutually. The lines in each family are parallel to a common plane, but not to each other. Hence the hyperbolic paraboloid is a. These properties characterize hyperbolic paraboloids and are used in one of the oldest definitions of hyperbolic paraboloids: a hyperbolic paraboloid is a surface that may be generated by a moving line that is parallel to a fixed plane and crosses two fixed.